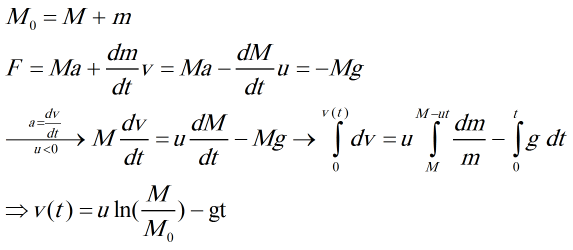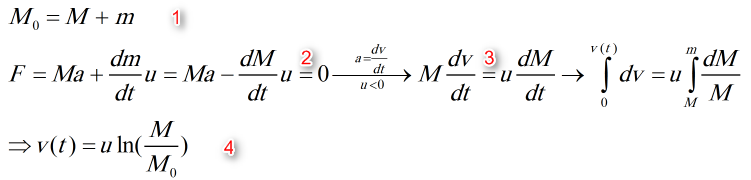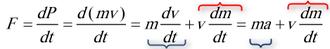مسئله ترکیب قرقره ها

 

• مسئله

مطابق شکل قرقره هایی آویزان شده اند،اگر قرقره ها و طناب ها اصطکاک و وزنی نداشته باشند؛شتاب وزنه ها را بیابید

 

 

• جواب 

طبق مسائل قبل ابتدا روابط مربوط به قانون دوم نیوتون را می نوسیم و سپس با پیدا کردن معادله قید ، جواب مسئله را پیدا می کنیم.

در اینجا بالا را جهت مثبت د رنظر گرفتیم.پس وزنه 2 رو به پایین می رود و وزنه 1 به سمت بالا حرکت می کند.

 

 

• تمرین

به عنوان تمرین می توانید مسئله را با فرض جرم دار بودن قرقره (3) حل کنید

(جرم قرقره را m در نظر بگیرید)

پاسخ خود را از برای ما بفرستید تا در صورت تایید رو سایت قرار گیرد

تماس با ما

در آینده پاسخ روی سایت قرار می گیرد

 

مسئله قرقره های روی میز

 

• مسئله

طبق شکل و داده های زیر سه قرقره به هم متصلند که دو تای افقی آن ها با سطح مسز اصطکاک دارند. اگر قرقره جرم ناچیزی داشته باشد؛نیروی کشش طناب متصل به جسم A و B را بیابید.

 

• جواب

مشابه مسئله قبل حل میکتیم با این تفاوت که در این حل ثابت بودن طول طناب و ثابت بودن جمع فاصله دو جسم بالایی از قرقره قید است

(واحد نیرو نیوتون و واحد شتاب متر بر مجذور ثانیه است) 

روابط قیدی : قرقره ها

روش حل مسئله قرقره متحرک و ثابت:

یکی از روش های بسیار کاربردی در حل قرقره ها استفاده از روابط قیدی است. در مطلب قبل گفتیم که برای حل قیدی باید یک قید پیدا کنیم. این قید در اینجا ثابت بودن طول ریسمان یا طناب است ( البته ما فرض می کنیم که طول طناب ثاب است)

برای شروع ابتدا جهت مثبت را به سمت بالا ( یا پایین) انتخاب می کنیم و سپس قانون دوم نیوتون (F=ma) را برای هر جسم جرم داری می نویسیم. حال نوبت معادله قید است: طول ریسمان ثابت است پس مجموع کار آن صفر است پس حال مقدار کار ها را با هم جمع می کنیم و سپس ساده می کنیم تا معادله جدیدی بدست بیاید و مجهول را پیدا کنیم.

(منتظر مثال ها باشید...)

روابط قیدی

برای یافتن جواب مسائل در نهایت به یک معادله نیاز داریم که مجهول را پیدا کنیم و عموما پیدا کردن این معادله سخت هست. در مسائل مکانیکی (مخصوصا مکانیک لاگرانژی)، یکی از روش ها پیدا کردن قیود هندسی است.کاهی پیدا کردن این قید بسیار ساده است و گاهی بسیار دشوار! مثلا می دانیم  طول میله ای که دو جعبه را به هم وصل کردند ثابت است پس دو جعبه همیشه فاصله ثابتی دارند و سرعت آنها برابر است یا مثلا طول ریسمان در قرقرهایی خاص ثابت است پس شتاب آن ها هم برابر است.

روش حل این مسائل اینگونه است که ابتدا با کمی دقت قید را پیدا کنیم و سپس آن را در کنار روابط فیزیکی قرار دهیم و با حل دستگاه معادلات به خواسته سوال برسیم.

(در آینده از این مسائل هم حل می کنیم؛ ان شاء الله)    

مسئله ستاره دنباله دار

 

• مسئله

در فضای تهی ستاره دنباله داری عجیب با سرعت اولیه V در حال حرکت است اگر در حین حرکت جرم دنباله دار طبق  تغییر کند؛سرعت آن را در زمان t بیابید

 

• جواب 

اولا باز هم با دو روش پایستگی تکانه را اثبات می کنیم 

روش اول 

روش دوم

سپس به حل این مسئله می پردازیم:

(واضح است که روش های گفته شده مشابه این روش هستند)

مسئله موشک در میدان گرانشی

 

• مسئله

(برگرفته از مثال 3-15 کتاب کلپنر )

موشکی به جرم M در فضا در یک میدان گرانشی در حال حرکت است. اگر سرعت اولبه موشک صفر و سرعت خروج گاز از موشک ثابت و برابر u باشد؛ رابطه ی سرعت و زمان موشک را بیابید.

 

• جواب

حل این مسئله هم بسیار شبیه مسئله قبل است فقط برایند نیرو ها در این مسئله صفر نیست.

برای توضیحات بیشتر می توانید به مسئله قبل مراجعه کنید.

 

 

 

(برگرفته از مثال 3-15 کتاب کلپنر )

مسئله موشک در فضای تهی

 

• مسئله

(برگرفته از مثال 3-14 کتاب کلپنر )

موشکی به جرم M در فضا بدون این که نیرویی به آن وارد شود در حال حرکت است. اگر سرعت اولبه موشک صفر و سرعت خروج گاز از موشک ثابت و برابر u باشد؛ رابطه ی سرعت و زمان موشک را بیابید.

 

 

• جواب

توضبحات (مهم):

1. M جرم موشک و در حال کاهش است ، m  هم جرم گاز آزاد شده است 

2.طبق سوال هیچ نیرو خارجی نداریم پس برایند نیرو ها صفر است.

3.اگر خواستید ببینید که  مشتق ها و انتگرال ها چگونه حل میشوند روی این لینک کلیک کنید.

4.دقت کنید  u منفی است. از این رو سرعت همواره مثبت است. 

5. کران بالای انتگرال جرم M است و کران پایین جرم اولیه است.  

(برگرفته از مثال 3-14 کتاب کلپنر )

 

 

نیرو , تکانه و حرکت موشک ها (تغییر جرم)

قبل پرداختن به مسئله حرکت موشک ها به مدل ساده تر آن یعنی بادکنک(!) می پردازیم. فرض کنید که باد کنکی را باد کرده اید و سپس رهایش می کنید؛ چه میشود؟ بادکنک فورا از دست شما خارج می شود و پرواز می کند پس حتما  به آن نیرو وارد شده است . ولی چه نیرویی؟ در مسائلی که در آن تغییر جرم داریم باید از تکانه استفاده کنیم.

طیق تعریف دقیقتر، نیرو برابر است با تغییرات تکانه در واحد زمان به عیارت دیگر نیرو همان مشتق تکانه نسبت به زمان است F=dP/dt و تکانه(P) هم برابر است با حاصل ضرب جرم در سرعت پس P=mv حال طبق قوانین مشتق و با در نظر گرفتن این که جرم هم تغییر می کند:

    

پس تغییر جرم هم ایجاد نیرو می کند و در موتور های جت ، فضاپیما ها و... بسیار کاربرد دارد و موشک ها هم برهمین اساس حرکت می کنند.

برای مطالعه بیستر کتاب کلپنر فصل 3 رو پیشنهاد می کنم البته بحث تکانه و تغییر جرم تقریبا در تمام کتاب های فیزیک پیدا می شود.

نیروی چسبندگی

جسمی که درون مایع یا گازی حرکت میکند، به دلیل تاثیر نیروی چسبندگی ناشی از شاره کند می شود. این نیروی چسبندگی بر خلاف اصطکاک در سطوح خشک،با سرعت وابستگی ساده ای دارد .یعنی متناسب است با سرعت حرکت. البته در سرعت های بالا نیرو های دیگر ناشی از اشفتگی هم وجود دارد و کل نیروی کند کننده وابستگی پیچیده ای پیدا می کند.( طراحان اتوموبیل های مسابقه ای برای محاسبه نیرو های کند کننده نیرویی متناسب با مربع سرعت بدست آورده اند)اما در بسیاری از موارد علمی ، چسبندگی تنها نیروی مهم کند کننده است.

چسبندگی از آنجا ناشی می شود که وقتی جسمی در محیطی حرکت می کند، نیرو هایی اعمال می کند که باعث حرکت شاره در طول جسم می شود. طبق قانون سوم نیوتون شاره نزدیک نیز یک نیرو عکس العمل وارد می کند.

نیروی بازدارنده چسبندگی را می توانیم به این شکل بنویسیم:

F = -Cv

  که در ان C  مقداری ثابت است که بستگی به جنس و شکل هندسی شاره دارد. F همواره در امتداد خط حرکت است. زیرا متناسب با v  است.علامت منفی هم جهت مخالف  F را نسبت به حرکت نشان می دهد. برای اجسامی با شکل ساده که از میان گاز با فشار پایین حرکت می کنند، C ر میتوان با اصول اولیه محاسبه کرد. ولی در کل  C را یک ثابت تجربی در نظر میگیریم.

کتاب آشنایی با مکانیک ، دانیل کلپنر ( چاپ یازدهم، صفحه 126)

قوانین کپلر

 

• قوانین کپلر

در سال 1609 ژوهانس کپلر سه قانون حرکت سیاره ای را در کتاب نجوم جدید منشر کرد. 

 

1-قانون اول: 

یک سیاره در یک مدا بیضی به دور خورشید می گردد. که خورشید یکی از کانون های بیضی است. 

 

2-قانون دوم:

خطی که سیاره را به خوشید وصل می کند در بازه زمانی یکسان مساحت های برابری را جاروب می کند.

 

3-قانون سوم;قانون هماهنگی:                   a³= P²

قانون سوم کپلر بیانگر این رابطه است که در آن P دور تناوب سیاره بر حسب سال و a میانگین فاصله سیاره و خورشید بر حسب AU (واحد نجومی) است

( یک واحد نجومی برابر با فاصله زمین تا خورشید است)

 

منبع : کتاب مقدمه ای بر اختر فیزیک جدید

 

( چاپ اول 1391 صفحه 33 و 34 )