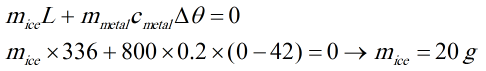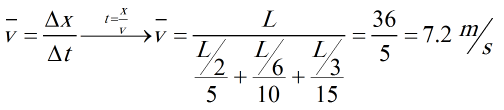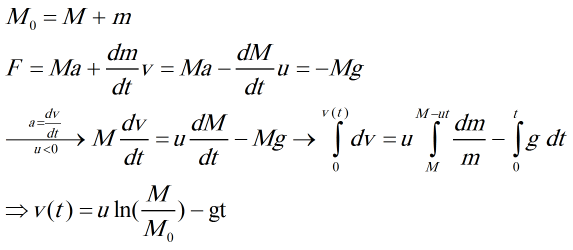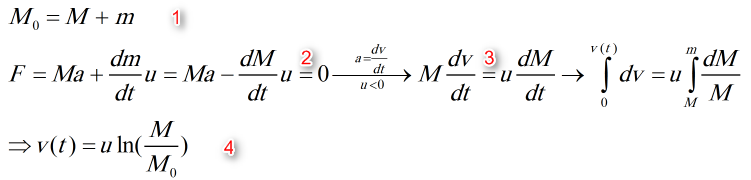- مسئله
در فضای تهی ستاره دنباله داری عجیب با سرعت اولیه V در حال حرکت است اگر در حین حرکت جرم دنباله دار طبق  تغییر کند؛سرعت آن را در زمان t بیابید
تغییر کند؛سرعت آن را در زمان t بیابید
- جواب
اولا باز هم با دو روش پایستگی تکانه را اثبات می کنیم
روش اول

روش دوم

سپس به حل این مسئله می پردازیم:
(واضح است که روش های گفته شده مشابه این روش هستند)

پایستگی تکانه:
در سیستم هایی که نیزوی خارجی وجود ندارد و به عبارت دیگر منزوی اند؛ تکانه کل ثابت است. بدون توجه به این که بر هم کنشهای بین ذرات سیستم منزوی چقدر قوی و حرکات آنان پیچیده باشد.
پایستگی تکانه در واقع بیان می کند که در تمام سیستم های منزوی تغییرات تکانه صفر است. این قانون بسیار در حل مسائل کاربرد دارد چرا که با اندکی تغییر آن را می توان به رابطه نیرو و تکانه رساند. می دانیم با مشتق گرفتن از تکانه ، نیرو بدست می آید:  حال اگر نیرو ما صفر باشد یا به عبارتی سامانه منزوی باشد (F=0) تغییرات تکانه برابر صفر میشود.(از این رابطه در مسائل قبلی نیز استفاده شده)
حال اگر نیرو ما صفر باشد یا به عبارتی سامانه منزوی باشد (F=0) تغییرات تکانه برابر صفر میشود.(از این رابطه در مسائل قبلی نیز استفاده شده)
- مسئله
یک گاری به جرم M محتوی مقداری آرد به جرم m است. در مبدا زمان از حال سکون با نیروی F کشیده می شود اکر به تدریج آرد با اندازه آهنگ ثابت b خارج شود؛ سرعت گاری را زمانی که همه آرد خارج شده بیابید
(مشابه مسئله 9-3 کلپنر)
- جواب
مشابه مسئله قبل اما کمی پیچیده تر...

- مسئله
یک واگن خالی به جرم M از حالت سکون تحت اثر نیروی F شروع به حرکت می کند. اگر در همین لحظه از قیفی که در امتداد مسیر در حال سکون قرار دارد با آهنگ b گندم به داخل واگن بریزد؛سرعت واگن را در زمان t بیابید.
(مشابه مسئله 10-3 کلپنر)

- جواب
ابتدا سخت به نظر می رسد ولی مسئله ی بسیار ساده ایست.
می خواهیم طبق روش دوم ( که در پست های قبلی توضیخ دادیم) حل کنیم:
ابتدا مقدار تکانه را در لحظه اول ویک لحظه بعد پیدا می کنیم و سپس در رابطه  جایگذاری می کنیم. البته در این مسئله کافیست لحظه اول و لحظه t را طبق این رابطه مقایسه کنیم.
جایگذاری می کنیم. البته در این مسئله کافیست لحظه اول و لحظه t را طبق این رابطه مقایسه کنیم.
البته مسائل تکانه اینجا متوقف نمیشوند...
مسائل جذاب تری در راه است... (-:
سوال و پیشنهاد :تماس با ما

در این مطلب به دو روش معمول حل مسائل تکانه در فیزیک کلاسیک می پردازیم
- روش اول
در این روش رابطه  را مینویسم و با توجه به داده ها و وقایع مسئله آن را حل میکنیم. این روش حل معروف تر است و بیشتر در مسائل ساده تکانه بدرد می خورد.در واقع ما تعریف تکانه ای نیرو را می نویسیم و F را برابر تمام نیرو های خارجی مثل گرانش،کولنی و... قرار می دهیم و در سمت دیگر تساوی با توجه به سرعت خروج جرم و سایر متغیر ها پارامتر ها را انتخاب می کنیم و با حل معادله، خواسته سوال ( مثلا معادله مکان زمان) را بدست می آوریم؛ لازم به ذکر است که در این مسائل عموما (نه همیشه!) به حل معادلات دیفرانسیلی بر میخوریم (مسئله شماره 8 و مسئله شماره 9 اینگونه حل شدند)
را مینویسم و با توجه به داده ها و وقایع مسئله آن را حل میکنیم. این روش حل معروف تر است و بیشتر در مسائل ساده تکانه بدرد می خورد.در واقع ما تعریف تکانه ای نیرو را می نویسیم و F را برابر تمام نیرو های خارجی مثل گرانش،کولنی و... قرار می دهیم و در سمت دیگر تساوی با توجه به سرعت خروج جرم و سایر متغیر ها پارامتر ها را انتخاب می کنیم و با حل معادله، خواسته سوال ( مثلا معادله مکان زمان) را بدست می آوریم؛ لازم به ذکر است که در این مسائل عموما (نه همیشه!) به حل معادلات دیفرانسیلی بر میخوریم (مسئله شماره 8 و مسئله شماره 9 اینگونه حل شدند)
- روش دوم
روش دوم تمام مسائل را حل میکند چراکه از خود تعریف تکانه نشات میگیرد. در این روش با توجه به شرایط مسئله عبارت P=mv (همان تعریف تکانه) را در دو زمان بسیار نزدیک می نویسیم و با رابطه نیرو و تکانه معادله را حل میکنیم. البته ابنجا هم به حل معادله دیفرانسیلی نیاز داریم . در آینده ان شاء الله چند مسئله ای را هم با این روش حل میکنیم.

در واقع هر دو روش یکی هستند اولی تعریف نیرو رو نوشته بعد حل میکنیم ولی در روش دومی مستقیم از روی تعریف تکانه حل میکنیم
- مسئله
متحرکی 1/2 مسیرش را با سرعت 5 متر بر ثانیه طی میکند و در 1/3 مسیر باقیمانده را با سرعت 10 متر بر ثانیه حرکت می کند. اگر سرعت منحرک در بقیه مسیر 15 متر بر ثانیه باشد؛سرعت متوسط را بیابید.
(ارسال شده توسط "M2ry2m")
- جواب
فرض می کنیم طول کل مسیر L است. از طرفی از روابط سینماتیک x=vt را میدانیم
دقت کنید! سوال در جمله دوم 1/3 ادامه مسر را گفته یعنی 1/6 کل مسیر.
- مسئله
موشکی به جرم M در فضا در یک میدان گرانشی در حال حرکت است. اگر سرعت اولبه موشک صفر و سرعت خروج گاز از موشک ثابت و برابر u باشد؛ رابطه ی سرعت و زمان موشک را بیابید.
- جواب
- مسئله
(برگرفته از مثال 3-14 کتاب کلپنر )
موشکی به جرم M در فضا بدون این که نیرویی به آن وارد شود در حال حرکت است. اگر سرعت اولبه موشک صفر و سرعت خروج گاز از موشک ثابت و برابر u باشد؛ رابطه ی سرعت و زمان موشک را بیابید.
- جواب